10-Solving Job Sequencing Problem with PyQUBO

この節では、Ising formulations of many NP problems から6.3. Job Eequencing with Integer LengthsをPyQUBOを用いて解きます。

整数長ジョブスケジューリング問題

整数長ジョブスケジューリング問題は以下のような状況の最適解を求める問題であり、NP困難な問題の一つです。まずは具体的な問から考えてみましょう。

具体例

分かりやすくするために具体的に以下のような問を考えます。 > 10個の仕事と3個のコンピュータがあります。10個の仕事の長さは\(1,2,\cdots,10\)です。 > どのようにコンピュータに仕事を割り振れば仕事にかかる時間の最大値\(\max M_\alpha\)を最小化できるか考えます。 > 例えば、\(V_1=\{9,10\},V_2=\{1,2,7,8\},V_3=\{3,4,5,6\}\)とすると\(\max(M_1,M_2,M_3)=19\)となって問の最適解となります。

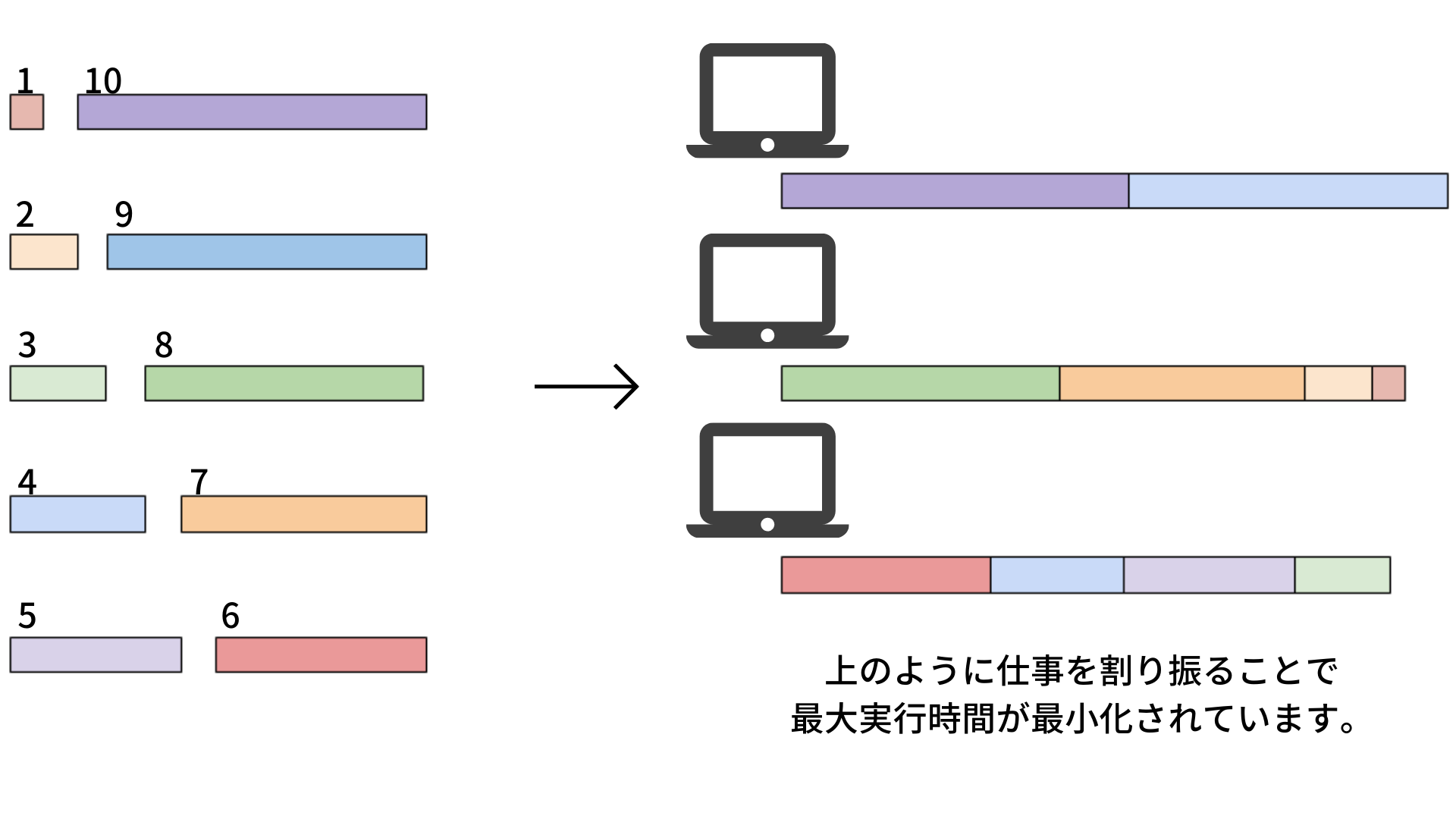
問題の一般化

まず、N個の仕事\(\{1,2,\dots ,N \}\)とm個のコンピュータがあるとします。各仕事が\(\alpha\)をindexとして持っているものと考えます。 仕事にかかる時間のリスト\(L\)を作ります。

\[L=\{L_1,L_2,\dots L_N\}\]

コンピュータ\(\alpha\)で行われる仕事の集合を\(V_\alpha\)としたとき、コンピュータ\(\alpha\)で仕事を終えるまでの時間は\(M_\alpha = \sum_{i\in V_\alpha} L_i\)となります。コンピュータ\(\alpha\)で行う仕事を表すバイナリ変数を\(x_{i,\alpha}\)としたとき、コンピュータが仕事を終わらすためにかかる時間の最大値は以下のように表すことができます。

\[max M_\alpha=M_1 = \sum_i L_ix_{i,1}\tag{1}\]

\[x_{i,\alpha}=\{0,1\}\tag{2}\]

\[(\forall \alpha \in \{1,2,\dots,N\})\]

この\(M_1\)を最小化することがこの問題の目的となります。

QUBO行列への変換方法

まず、\(M_1 = \max M_\alpha\)として一般性を失わないことに注意します。 8-Solving Knapsack Problem with PyQUBOでも解説されているようにQUBO行列を表現するにあたって式(1)で定義したバイナリ変数\(x_{i,\alpha}\)に加えてコンピュータが仕事にかかる時間を表現するためのスラック変数yを導入します。

One-hot encoding により仕事にかかる最大値と他との差を表現した制約項(2)の定義

Ising formulations of many NP problems ではOne-hot encodingを用いて仕事の実行時間を表しています。 バイナリ変数\(y_{n,\alpha}\)をノード1とノード\(\alpha\)の仕事の長さの差を表すバイナリ変数とします。

\[\begin{split}y_{n,\alpha} = \begin{cases} 1 & (M_1-M_\alpha = n,\alpha\neq 1,n\geq 0) \\ 0 & (otherwise) \end{cases}\end{split}\]

よってコンピュータ\(\alpha\)の実行時間がコンピュータ1の実行時間より短い点に関して以下の式が成り立たなければなりません。

\[\sum_{n=0}^{\mathcal{M}}ny_{n,\alpha} = \sum_{i=1}^N L_i(x_{i,1}-x_{i,\alpha})\tag{7}\]

\[H_{A1} = A\sum_{\alpha=2}^m\left(\sum_{n=0}^{\mathcal{M}}ny_{n,\alpha} - \sum_{i=1}^N L_i(x_{i,1}-x_{i,\alpha})\right)^2\tag{8}\]

このようにハミルトニアンを定めることでエネルギーが最小となった際にこの制約を満たすようなスピン状態を得ることができます。

そして\(\alpha\)を固定したときにただ一つだけの\(y_{n,\alpha}\)だけが1となり、他は0となる必要もあります。

\[H_{A0} = A\left(1-\sum_{n=0}^{\mathcal{M}}y_{n,\alpha}\right)^2\tag{9}\]

更に、ある仕事iはいずれか一つのコンピュータで行われるという制約も加える必要があります。

\[H_{A2} = A\left(1-\sum_{i=1}^{N}x_{i,\alpha}\right)^2\tag{10}\]

これらを踏まえるとハミルトニアンの制約項全体は正の定数\(A\)を用いて次のように定義されます。

\[H_A = A(H_{A0}+H_{A1})+AH_{A2}\tag{11}\]

\(\mathcal{M}\)はユーザーによって選ばれる値であり、コンピュータ\(\alpha\) とコンピュータ1の差がどの程度存在するか表しています。最悪の場合\(\mathcal{M}\)は\(N\max L_i\)となります。

Log encoding によるスラック変数を用いた制約項(2)の定義

8-Solving Knapsack Problem with PyQUBOのようにLog encodingを用いて制約項を設定してみましょう。 \(\mathcal{M}\)はコンピュータ1とコンピュータ\(\alpha\)の仕事の実行時間の差の上限であるため以下の不等式が成り立ちます。

\[\mathcal{M}\geq \sum_{i=1}^N L_i(x_{i,1}-x_{i,\alpha}) = M_1-M_\alpha\tag{13}\]

ここでコンピュータで行われる仕事が一つ以上割り振られ、仕事量が1以上であるとします。するとスラック変数Yを\(0\leq Y \leq \mathcal{M}-1\)を満たすとして定義することができます。

上記不等式(13)は等式制約に変換できると分かります。

\[\mathcal{M} = Y + M_1-M_\alpha\tag{14}\]

スラック変数Yを具体的に記述すると以下のようになります。

\[Y = \sum_{n=1}^{\lfloor\log_2(\mathcal{M}-1)\rfloor} 2^n y_n\tag{15}\]

式(12)の第一項、第二項は以下の項に置き換えることができます。

\[\sum_{\alpha=2}^m \left(\mathcal{M}-\sum_{i=1}^N L_i(x_{i,1}-x_{i,\alpha}) - \sum_{n=1}^{\lfloor\log_2(\mathcal{M}-1)\rfloor} 2^n y_n\right)^2\tag{16}\]

この方法を用いると、One-hot encodingに比べて少ないバイナリ変数\((\lfloor\log_2(\mathcal{M}-1)\rfloor+1)\)個で整数を表現できる上に追加の制約項が不要になります。変数Yの最大値は\(2^{\lfloor\log_2(\mathcal{M}-1)\rfloor}\)となっているからです。また、スラック変数を用いているため、仕事量の差が\(\mathcal{M}\)を上回ることもありません。

目的項(1)の定義

目的項はコンピュータで仕事を終えるまでの最大実行時間を最小化するためのものです。 よってハミルトニアンは以下のように定義するとエネルギーが最小になったときに最大実行時間を最小化した解が得られます。

\[H_B = B\sum_{i=1}^N L_ix_{i,1}\tag{17}\]

ただし定数A,Bは目的項\(H_B\)によって制約項\(H_A\)を違反してはいけないため、\(0<B \max(L_i)<A\)を満たす必要があります。

PyQUBOへの実装

PyQUBOのDocumentationでは、バイナリ変数を整数に変換するための4つのクラスについて説明されています。その中のLogEncIntegerを用いてスラック変数を定義します。 8-Solving Knapsack Problem with PyQUBOであるようにLogEncIntegerの使い方は以下のようになっていて、整数のように扱うことができます。

y = LogEncInteger("ラベルの名前",最小値,最大値)

この時、yがとりうる値の最大値は上で指定した数ではなく,\(2^{\lfloor\log_2(\mathcal{M}-1)\rfloor+1}\)となることに注意してください。 #### QUBO行列の生成 では、具体例で示した問題を実際にQUBO行列にしてPyQUBOで解いてみましょう。 まず、仕事の個数Nとコンピュータの数m,仕事の長さのリストLを定義します。

import numpy as np
#コンピュータの数
m=3
#仕事の長さ
L= [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
#仕事の数
N=len(L)

\(\mathcal{M}\)を選び、Mに代入します。

M = 3

次にバイナリ変数を定義します。スラック変数yに対しては先ほどのLogEncInteger()を使います。

#PYQUBOをimportします
from pyqubo import Array,LogEncInteger

x = Array.create('x', shape=(N,m), vartype='BINARY')
y =  LogEncInteger('y',(0,M))

上の変数を用いて式(10),(16),(17)に従ってハミルトニアンを定義します。

\[H_{A1} = A\sum_{\alpha=2}^m \left(\mathcal{M}-\sum_{i=1}^N L_i(x_{i,1}-x_{i,\alpha}) - \sum_{n=1}^{\lfloor\log_2(\mathcal{M}-1)\rfloor} 2^n y_n\right)^2\]

\[H_{A2} = A\left(1-\sum_{i=1}^{N}x_{i,\alpha}\right)^2\]

\[H_A = AH_{A1} + AH_{A2}\tag{18}\]

しかし,式(18)のハミルトニアンでは良い解が得られません。 そこで\(H_A\)の項をそれぞれ異なる係数に分解し、それぞれ設定することにしましょう。

\[H_A = A_1H_{A1} + A_2H_{A2}\]

\[H_B = B\sum_{i=1}^N L_ix_{i,1}\]

\(A_1,A_2,B\)は\(0<B \max(L_i)<A_1,A_2\)を満たすように選びます。それぞれの大小のバランスは係数がかかっている項のスケールが均等になるように調節します。

from pyqubo import Constraint
A2=36

A1=(A2/max(L) **2)/0.12

B = (A2/max(L))/3.6

# ハミルトニアンの第一項
const = 0
for a in range(1,m):
    const += (M - sum([L[i]*(x[i,0]-x[i,a]) for i in range(N)])-y)**2
HA1 = Constraint(const, label='HA1')

# ハミルトニアンの第二項
HA2 = Constraint(sum((1-sum(x[i,a] for a in range(m)))**2 for i in range(N)), label='HA2')

# ハミルトニアンの第三項
HB = sum(L[i] * x[i,0] for i in range(N))

# ハミルトニアン全体を定義します
Q = A1*HA1+A2*HA2+B*HB

上記の式をPyQUBOで解かせた結果を見てみましょう。 brokenはペナルティ項が破れているとき(0でないとき)、どのように破れたかを記録してくれます。brokenが{}であると、制約が破られていないと分かります。

from pyqubo import solve_qubo

model = Q.compile()
qubo, offset = model.to_qubo()

# nealを用いて使います
import neal
sampler = neal.SimulatedAnnealingSampler()
raw_solution = sampler.sample_qubo(qubo, num_reads=500)
decoded_sample = model.decode_sample(raw_solution.first.sample, vartype="BINARY")
#結果の表示
print("[Inputs]")
print()
print("N (仕事の数) : "+str(N)+"個")
print("m (コンピュータの数): "+str(m))
print()
print("仕事の長さのリスト")
print(L)
print()
print("A1 : "+str(A1))
print("A2 : "+str(A2))
print("B : "+str(B))
print()
print("[Results]")
print()
job_length = [0] * m
for i in range(0,m):
    print("コンピュータ"+str(i+1)+"で行われる仕事")
    for j in range(0,N):
        if decoded_sample.array('x', (j,i))==1:
            print(str(j+1)+"番目の仕事 長さ:"+str(L[j]))
            job_length[i] += L[j]
    print("仕事の総実行時間:"+str(job_length[i]))
    print()

print("broken")
print(decoded_sample.constraints(only_broken=True))

[Inputs]

N (仕事の数) : 10個
m (コンピュータの数): 3

仕事の長さのリスト
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

A1 : 3.0
A2 : 36
B : 1.0

[Results]

コンピュータ1で行われる仕事
2番目の仕事 長さ:2
3番目の仕事 長さ:3
6番目の仕事 長さ:6
8番目の仕事 長さ:8
仕事の総実行時間:19

コンピュータ2で行われる仕事
1番目の仕事 長さ:1
7番目の仕事 長さ:7
10番目の仕事 長さ:10
仕事の総実行時間:18

コンピュータ3で行われる仕事
4番目の仕事 長さ:4
5番目の仕事 長さ:5
9番目の仕事 長さ:9
仕事の総実行時間:18

broken
{}

OpenJijに投げる

次にOpenJijのSQAを用いて解いてみます。量子力学的振る舞いを再現するため、計算に必要な時間は前と比べて多少伸びます。

# OpenJijのインポートをします
import openjij as oj
# SQAを使います。
sampler = oj.SQASampler()
# PYQUBOで使ったquboを使います。
response = sampler.sample_qubo(Q=qubo, num_reads=300)
# エネルギーが一番低い状態を取り出します。
dict_solution = response.first.sample
# デコードします。
decoded_sample = model.decode_sample(raw_solution.first.sample, vartype="BINARY")
#結果の表示
print("[Results]")
print()
job_length = [0] * m
for i in range(0,m):
    print("コンピュータ"+str(i+1)+"で行われる仕事")
    for j in range(0,N):
        if decoded_sample.array('x', (j,i))==1:
            print(str(j+1)+"番目の仕事 長さ:"+str(L[j]))
            job_length[i] += L[j]
    print("仕事の総実行時間:"+str(job_length[i]))
    print()

print("broken")
print(decoded_sample.constraints(only_broken=True))

[Results]

コンピュータ1で行われる仕事
2番目の仕事 長さ:2
3番目の仕事 長さ:3
6番目の仕事 長さ:6
8番目の仕事 長さ:8
仕事の総実行時間:19

コンピュータ2で行われる仕事
1番目の仕事 長さ:1
7番目の仕事 長さ:7
10番目の仕事 長さ:10
仕事の総実行時間:18

コンピュータ3で行われる仕事
4番目の仕事 長さ:4
5番目の仕事 長さ:5
9番目の仕事 長さ:9
仕事の総実行時間:18

broken
{}

まとめ

Job Eequencing with Integer LengthsをPyQUBO,OpenJijを使って解く方法について解説しました。

係数を調整する前では良い解が得られませんが係数を調整すると安定しました。

また、整数をバイナリ変数で表現する方法は複数ありますが、今回はLog encodingを扱いました。 8-Solving Knapsack Problem with PyQUBOと合わせて確認してみてください。